Publications
The classical serendipity and mixed finite element spaces suffer from poor approximation on nondegenerate, convex quadrilaterals. In this paper, we develop families of direct serendipity and direct mixed finite element spaces, which achieve optimal approximation properties and have minimal local dimension.
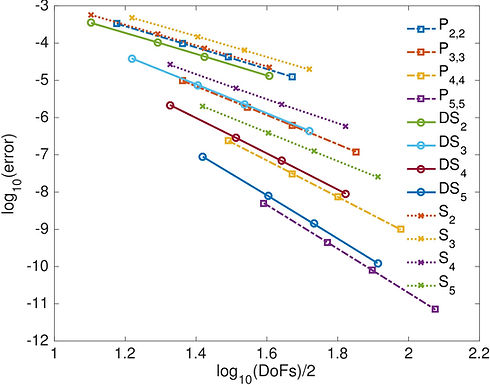
We construct new families of direct serendipity and direct mixed finite elements on general planar, strictly convex polygons that are H1 and H(div) conforming, respectively, and possess optimal order of accuracy for any order. They have a minimal number of degrees of freedom subject to the conformity and accuracy constraints.

We construct direct serendipity finite elements on general cuboidal hexahedra, which are H1-conforming and optimally approximate to any order. They have minimal degrees of freedom subject to conformity and accuracy constraints.

We propose alternative ways to construct the supplemental functions on the element as continuous piecewise polynomials. The new piecewise polynomial supplements can be integrated accurately, and therefore show better robustness concerning the underlying meshes used.

